Článek
Přes čtyřicet let jsem se živil výukou matematiky snad na všech typech škol. Již nějakou dobu ale dění ve školství téměř nesleduji. Proto jsem letos na jaře jen periferně zaregistroval, že byly opět nějaké problémy s maturitou z matematiky. Další pozornost jsem tomu tehdy nevěnoval, protože tyto problémy se opakují rok co rok.
Chvíli se jako každý rok brblalo, že maturita byla těžká a vyžadovala „neobvyklé postupy“. Tím to zhaslo.
Teprve až teď a čirou náhodou jsem zjistil, o co letos vlastně šlo, a rozum mi zůstal stát. To nebyla běžná chyba, kterou občas uděláme všichni. Letos Cermat věru netroškařil. Nezdržoval se s jindy obvyklými terminologickými neznalostmi, nejednoznačným zadáním apod. Letošní „neobvyklý postup“ byl čelním útokem na základy matematické logiky. Úloha 25A je přímo kabinetní ukázkou toho, jak matematická úloha a její řešení vypadat nesmí.

Maturitní úloha 2025
(lze najít zde)
Maturant má tedy v podstatě jen vyřešit šest kvadratických rovnic. Něco takového se ale autorům maturitního testu asi zdálo moc jednoduché, a tak to prvními čtyřmi řádky zahalili do mlhy husté tak, že by se dala krájet, a pak se v té mlze sami ztratili. A to hned dvakrát.
V mlze se má bloudit velmi opatrně, takže velmi podrobně a nejlépe slepeckou holí nejdříve osaháme okolní terén.
Co v tomto zadání znamená slovo "řešení"? U jiné úlohy má student do záznamového archu uvést celý „postup řešení“. Je tedy řešení totéž, co nějaký „postup"? Anebo snad jen poslední krok tohoto „postupu“? V kontextu zadání úlohy 25 ani jedno, ani druhé. Ani postup, ani žádný jeho krok totiž do žádného intervalu asi patřit nebude.
Takže co? „Řešením rovnice“ tak, jak ho chápe zadání, může být za třetí každé číslo, které dosazeno do této rovnice ji změní v pravdivou rovnost. V tom případě by neměl autor matematického textu používat slovo řešení, ale kořen. Bylo by jasno. Ale taková nuance je zřejmě pod rozlišovací schopností „odborníků“ z Cermatu.
Konečně za čtvrté - řešením rovnice je podle mnohých středoškolských učebnic množina všech jejich kořenů.
Takže, milý maturante, vyber si. Odpověď na otázku úlohy 25 totiž zcela závisí na tom, který ze čtyř významů slova „řešení“ si zvolíš.
Nezpochybnitelné autority z Cermatu si vybraly možnost pátou. Tito experti totiž moc nepřemýšleli, v textu Vyřešené zadání pro didaktický test z matematiky - jaro 2025 původně do kolonky „řešení úlohy 25 A“ napsali „úloha nemá řešení“ a rovnici A „nepřiřadili“ k žádnému ze dvou intervalů. Na to konto všechny studenty, kteří přemýšleli jinak, obrali o body a naivně se domnívali, že jsou ze své vlastní mlhy venku.
Pak se ale asi našel nějaký filuta, kterému nejspíš chyběl bod, odvolal se a zřejmě dovedně zažongloval pojmem prázdná množina. Poté se určitě sešla nějaká učená komise, která začala to odvolání zkoumat.
Těžko říct, který alchymista jako první zpatlal dohromady dva výše uvedené významy stále nevysvětleného pojmu „řešení“ a začal ve svém hrnci usilovně míchat predikát náležení s predikátem inkluze. Někdo si pak ještě nejspíš nechal poslat pro babí hněv, laskavec a čimeřici, aby od časného rána pražil na tom lomikámen. Nevyrobil sice ani zlato, ani elixír mládí, ale extrahoval skvostnou perlu, kterou Cermat nazval druhé řešení:
„Do obou možností 25.1 a 25.2 je možné doplnit také možnost A. Prázdná množina je totiž podmnožinou každé množiny“ (možno nahlédnout zde) .
Do kouře dýmovnice, kterou nastražil na studenty, se zadavatel zamotal podruhé a to tak, že nejspíš definitivně, protože toto „řešení“ v oficiálních dokumentech letošní maturity k dnešnímu dni (23.8.2025) stále je. Kdybych takto „vyřešil“ tuto úlohu před padesáti lety v prvním ročníku gymnázia já, byl bych pro výstrahu zastřelen před nastoupenou sborovnou.
Zkusme tedy v té mlze najít nějakou cestu. Předpokládejme, že pojmem „řešení rovnice“ se rozumí množina všech jejich kořenů. Není sice jasné, proč v tomto případě zadání mluví o „všech řešeních“, když takovéto řešení má každá rovnice vždycky právě jedno, ale budiž - tato vada je jen kosmetická. Pak je sice pravda, že řešením rovnice A) je prázdná množina a že prázdná množina je podmnožinou každého intervalu, tedy
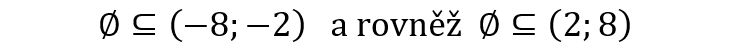
inkluze
ale na to se úloha přece neptá! Úloha se neptá na podmnožinu. Úloha se ptá, zda řešení do intervalu patří, tedy zda platí
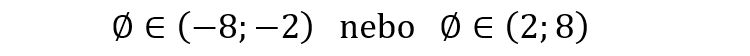
náležení
Ani jedno z toho samozřejmě neplatí. A nebude to platit dokonce ani tehdy, když místo prázdné množiny napíšeme jakoukoliv množinu jinou. Takže pokud je řešením rovnice množina kořenů, nelze podle zadání příkladu 25 ani jednomu intervalu přiřadit ani jednu rovnici. Úlohu v tomto případě tedy správně řešil jenom ten, kdo ji vůbec neřešil. Nechal ji nevyplněnou a nepřiřadil nikam ani žádnou z rovnic B), C), D), E) a F).
Co když se tedy „řešením rovnice“ myslí jeden její kořen?
Může neexistující kořen patřit do existujícího intervalu?
Jestliže ano, musím být schopen nějak ukázat, kde v tom intervalu je, anebo (což je matematicky totéž) ho z toho intervalu „vybrat“ tak, jak vybírám například míček z osudí. Stojíme tedy před vpravdě cimrmanovským problémem vybrat z osudí míček, který vůbec neexistuje. Jára Cimrman by to určitě dokázal, ale já to neumím a obávám se, že ani černokněžníkům z Cermatu se to nepodaří.
Přesto bych nevylučoval, že se příští rok maturanti setkají třeba s touto úlohou:
Zjistěte, která osobnost je vyobrazena na české stopadesátitříkoruně:
a) žádná b) Spiderman c) Superman d) Rumcajs e) Rákosníček f) Vochomůrka
Původní autorské řešení: a) žádná, protože taková bankovka neexistuje
Oprava po odvolání: Množina všech stopadesátitříkorunových bankovek je prázdná a prázdná množina je podmnožinou každé množiny. Tedy i množiny všech políček filmů o Rákosníčkovi, na kterých je Rákosníček zobrazen. Úloha má tedy dvě možná řešení, tím druhým řešením je možnost e) Rákosníček.
Správně samozřejmě není ani jedna z nabízených možností. Ani u úlohy fiktivní, ale ani u skutečné 25A. Kdysi jsme se už v prvním ročníku gymnázia učili, že z nepravdivých předpokladů lze i správným úsudkem vyvodit jakýkoliv, tedy i zcela nesmyslný závěr. A právě to udělal Cermat v případě úlohy 25A. Z nepravdivého předpokladu, že nějaké x patří do prázdné množiny, „vyvodil“ jeden z nekonečně mnoha nesmyslů, které vyvodit mohl, a v opravené verzi (zde) oficiálně deklaroval, že právě tento jeho nesmysl je hledanou pravdou.
Jeden ze základních zákonů logiky říká, že mají-li existovat všichni, pak musí existovat alespoň někdo. Je to zákon partikularizace. Je-li někomu příjemnější jeho logická obměna, pak tedy: neexistuje-li nikdo, pak neexistují ani všichni. Pro fajnšmekry:
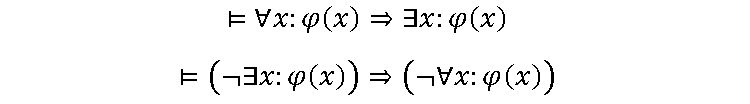
zákon partikularizace a jeho obměna
Cermat místo toho vymyslel
zákon cermatizace: neexistuje-li nikdo, znamená to, že existují všichni.
Učitelé, pomalu se učte psát:
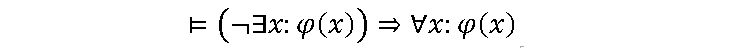
zákon cermatizace
Cermatizace středního školství nejspíš postupuje mílovými kroky, takže možná, že zákon cermatizace zanedlouho bude i ve vzdělávacích plánech. Zatím to tam ale neproniklo, takže letos na jaře bylo možné na úlohu 25 reagovat jediným způsobem: úloha je v části A) nekorektní, takže ji nelze řešit.
Chyby děláme všichni. Ale je s podivem, že původní chyba nejenže prošla bezpočtem kontrol, ale že komise složená z vystudovaných matematiků(?) schválila její následnou explicitní „opravu“. Ta už není jen chybou, ale dobrovolně přiznanou nevzdělaností.
Letošní maturitou a zejména následnými kroky se Cermat úplně odkopal. Je to partička neumětelů, která neovládá ani středoškolskou matematiku a která slovo logika zřejmě v životě neslyšela.
Ten, kdo nutí studenty k úsudkům vycházejícím z nepravdivých předpokladů, úsudkům o vlastnostech neexistujících objektů, navíc při dosud nejzávažnější zkoušce jejich života, nejenže prokazuje fatální neznalosti základů matematiky, ale působí ve znalostech i psychice nastupující generace nenapravitelné škody.
Cermat by měl studenty k maturitě z matematiky lákat. Svými nekompetentními a absurdními kroky však dělá pravý opak – mladé generaci matematiku stále více znechucuje.
Jak dlouho ještě bude tento gang diletantů našim středním školám vládnout? Přestane se snad opravdu na středních školách učit logika matematická a jako součást tréningu na maturitu nastoupí logika cermatovská? To se vážně ještě nenašlo žádné dítě, které by zvolalo, že tento náš všemocný vládce maturit je úplně nahý?



