Článek
Ano, mluvím o legendární, všemocné trojčlence! Kdysi bývala hvězdou matematických sešitů na základních školách, dnes aby ji člověk hledal lupou v zaprášených osnovách, pokud tam tedy vůbec ještě straší. A to, že se na ni všeobecně zapomnělo, je, milí přátelé, tragédie srovnatelná se zjištěním, že máte flek na posledním tričku ve chvíli, kdy chcete jít na rande.
Co to vlastně ta trojčlenka byla (a pro pamětníky stále je)?
Představte si trojčlenku jako takového matematického superhrdinu pro každodenní život. Máte tři známé hodnoty a potřebujete zjistit tu čtvrtou, záhadnou. Je to jako detektivka, kde indicie vedou k jasnému pachateli – výsledku!
Potřebujete třeba vědět, kolik mouky koupit na pět bábovek, když na dvě bábovky stačí půl kila? Trojčlenka! Zajímá vás, za jak dlouho tři malíři vymalují byt, když jednomu by to trvalo týden a vy jste pozvali tchyni na nedělní oběd? Trojčlenka! (A možná i rychlokurz asertivity). Chcete spočítat, kolik piv stihnete vypít za večer, když první dvě zmizela za půl hodiny a hospoda zavírá za další tři? Trojčlenka! (I když tady už může hrát roli nepřímá úměra vaší soudnosti).
Jak to fungovalo? Ta brilantní jednoduchost!
Vzali jste si ty tři známé údaje, chytře je poskládali pod sebe a vedle sebe, udělali pár křížových operací, které vypadaly jako tajné znamení zednářů, a voilà! Výsledek byl na světě. Bylo to tak uspokojivé, jako když vám konečně zapadne poslední dílek puzzle.
Proč ta nostalgie a lehké rozhořčení? Protože slovní úlohy jsou dneska španělská vesnice nejen pro děti, ale i pro mnohé dospělé!
Ruku na srdce, kdo z nás dneska nepoužívá trojčlenku, byť třeba jen intuitivně? Přepočítáváme slevy v obchodě („Když po slevě 30 % to stojí tolik, kolik je původní cena?“), plánujeme čas na cestu („Jestli 100 km ujedu za hodinu, za jak dlouho budu v Horní Dolní, která je 250 km daleko?“), příkladů je hromada. Tyhle kupecké počty děláme pořád a pořád.
A teď si představte tu hrůzu: dnešní děti, které (až na opravdu nepočetné výjimky) o trojčlence slyšely jen jako o nějakém prehistorickém nástroji, jako je pazourek nebo disketa. Jak si poradí s nástrahami běžného života? Jak mají, proboha, pochopit jednoduchou slovní úlohu, když jim chybí ten základní kámen logického úsudku, kterým trojčlenka je? Když jim zadáte, že „Pepa natrhá za hodinu 3 kila jablek a Lojza 2 kila, za jak dlouho společně natrhají 10 kilo?“, koukají na vás, jako byste po nich chtěli vysvětlit teorii relativity pozpátku. Bez trojčlenky (nebo alespoň myšlenkového postupu, který k ní vede) jsou tyhle úlohy pro ně čiré sci-fi. Budou odkázány na aplikace v mobilech, které jim jako novodobé božstvo milostivě něco odpoví, ale nevysvětlí tu krásu a logiku, která se za výpočtem skrývá? A nebudou schopné si ani přibližně ověřit, jestli jim božstvo náhodou nekecá? Svět se řítí do záhuby, říkám vám!
Návod na trojčlenku i pro ty, co matematiku viděli naposledy v minulém století, a ještě z rychlíku (alias „Trojčlenka pro telecí“)
Nebojte, není to žádná věda, i když to tak možná na první pohled vypadá. Pojďme na to hezky polopatě:
Krok 1 - Rozmysli si, jestli je to úloha typu „čím víc, tím víc“, ANEBO „čím víc, tím míň“. Tohle je klíčové!
- Přímá úměra („čím víc, tím víc“): Když přidám jedné věci, přidá se i druhé. Například:
- Čím víc rohlíků koupím, tím víc zaplatím.
- Čím déle pojedu autem (stejnou rychlostí), tím dál dojedu.
- Nepřímá úměra („čím víc, tím míň“): Když přidám jedné věci, druhé naopak ubude. Například:
- Čím víc malířů bude malovat byt, tím méně času jim to zabere.
- Čím rychleji pojedu, tím méně času mi cesta zabere.
Krok 2 - Napiš si, co víš, hezky pod sebe a vedle sebe na kus papíru.
- Vždycky piš stejné věci pod sebe. Třeba hodiny pod hodiny, kusy pod kusy.
- Neznámou věc (to, co chceš spočítat) označ třeba písmenem X:

Krok 3 - A teď už jen počítej jako pán (nebo dáma)!
Typ úlohy PŘÍMÁ ÚMĚRA (to bylo to „čím víc, tím víc“):
Příklad: Za 2 hodiny ujedu 100 km. Kolik km ujedu za 3 hodiny (stejnou rychlostí)?
Nakresli si šipky. Je mnoho variant, já používám tuhle:
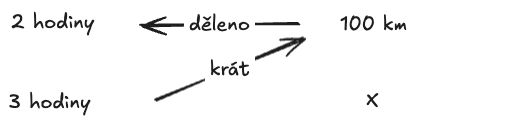
Vzoreček pro šprty: X = (B1 x A2) / A1
Výpočet: X = (3 × 100) / 2 = 300 / 2 = 150
Výsledek: Za 3 hodiny ujedu 150 kilometrů.
Jak elegantní, jak logické (více času, více kilometrů), jak jednoduché!
Typ úlohy NEPŘÍMÁ ÚMĚRA (to bylo to "čím víc, tím míň"):
Příklad: 3 malíři vymalují byt za 10 hodin. Za jak dlouho vymaluje byt 5 malířů?
Tady se šipky kreslí jinak, ale postup výpočtu je pak stejný:
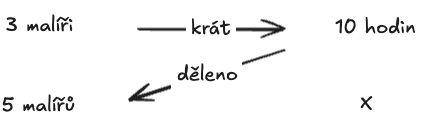
Vzoreček pro šprty: X = (A1 x A2) / B1
Výpočet: X = (3 × 10) / 5 = 30 / 5 = 6.
Výsledek: 5 malířů vymaluje byt za 6 hodin.
(Taky logické, víc lidí, méně času).
Krok 4 - Zkontroluj si to selským rozumem! Dává ti výsledek smysl? Pokud ti vyšlo, že pět malířů bude malovat déle než tři malíři, asi je někde chyba (nebo se flákají). Zkus to znovu a použij správnou variantu šipek.
Krok 5 - … žádný není, máš hotovo!
Tak co, není ta trojčlenka vlastně docela prima kámoška?
Možná je to jen můj staromilský povzdech, ale trocha té základní logiky zabalené do elegantního hávu trojčlenky by dnešní mládeži rozhodně neuškodila.
Takové malé krůčky totiž budují civilizace, nebo - pokud jsou dělány vzad - civilizace boří.
Co myslíte, neměli bychom sepsat petici za „Návrat trojčlenky na výsluní českého školství“? Než bude pozdě?






