Článek
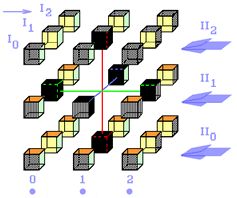
Bodová 3D krychle
Předpokládáme (víme?), že žijeme v lineárním – rovnoměrném prostoru. Jenže tento Euklidův prostor je plný nevypočitatelných iracionalit. Kdysi se mne profesor N. z Masarykovy univerzity zeptal – „Co vám na těch iracionalitách tak vadí?“
Jejich naprostá nepřesnost! Nerozumím, jak mohou přibližné výsledky nevadit. V technice budiž, zaokrouhlíme. Ale proč také věda nebádá nad nepřesnými výsledky? Vždyť náhrada se nabízí - podle předchozího dílu je to zraková perspektivní geometrie.
A co víc, je slučitelná (kompatibilní) s bodovou (diskrétní) geometrií. Takovou, jejíž podstata (princip) je shodná s informatickou databází u počítačů.
Je ovšem srozumitelné, že zavedením iracionalit dosáhla věda zásadních úspěchů. Počínaje Newtonem, až k velikánům 20. století a s vyvinutou technikou.
Na matematickou přesnost perspektivního prostoru navazuje prostor bodový. V něm se vzdálenosti počítají pravoúhlými kroky.

Barevné body tvoří čtverec
Všechny barevné body mají stejnou vzdálenost od počátku, čtyři kroky. Takže čtverec, postavený na vrchol, je kružnicí diskrétního prostoru. Vyhovuje její definici.
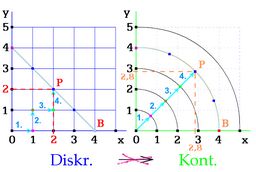
Převod bodu mezi prostory - nezdar
Zde se ukazuje, že prostor Euklidův nenavazuje na šachovnicovou síť, tedy na diskrétní prostor.
Například bod P se souřadnicemi [x=2, y=2] v bodovém prostoru se sice nachází ve spojitém (kontinuálním) Euklidově prostoru opět ve vzdálenosti 4 - jenže má jiné souřadnice, přibližně [2,8; 2,8].

Převod bodu mezi prostory - zdar
Jinak s převodem z diskrétního prostoru do perspektivy, například pro bod T [x=1, y=3]. Převod vyhovuje, v obou prostorech má bod stejné souřadnice a vzdálenost od počátku.

Shoda při převodu bodu mezi prostory
Bod C [x=2, y=3] prokazuje přesnou návaznost bodového a perspektivního zrakového prostoru. Od počátku je v obou prostorech stejně vzdálený: 5.

Každý pozorovatel je středem svého systému
Pozorovatel je v počátku, bod K. Pak přejde z počátku K [0;0] do bodu J [x=1; y=0] na vodorovné ose. Jak se změní jeho zrakový vjem?
Pozorovatel v bodě K měl ke kolegovi v bodu J vzdálenost 1. Potom k dalšímu bodu I je vzdálenost 2. A ta platí i na dolním obrázku. Snad pozorovatel v bodě J se domnívá, že vzdálenost K-I je moc velká? Odpověď:
Vraťme se k bodovému obrázku vlevo. A vidíme, že vzdálenosti jsou pevné, pouze zraková perspektiva je mění.
Proto ji máme podcenit? Odmítnout? Ne! Vždyť dává vždy racionální výsledky.
Přijatelnost takto zavedeného obrazu našeho světa se v tomto obhajuje.

Dva prostory v síti
Navíc i perspektivu lze vybavit přesnou prostorovou sítí. Takže návaznost obou prostorů nabízí našemu světu, perspektivnímu světu, že všechny jeho prostorové body mají celočíselné souřadnice.
Zorné úhly
Velikost objektů v lidském vnímání optika posuzuje zorným úhlem.

Velikosti zorných úhlů
V obrázku s milimetrovou sítí jsou zakresleny i vodorovné barevné úsečky, jejichž délka značí velikost zorného úhlu. Zde bez dalších souvislostí.
Rozpor
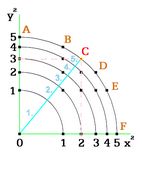
Nerovnoměrně rozložené body A-F
Na obrázku však sledujeme i rozpor se skutečnými vjemy našeho zraku. Sousední body, které leží na společné kružnici, se liší svou vzájemnou vzdáleností. Velký je rozdíl vždy u prvního bodu na oblouku, jenž je nejblíž ose. Tedy obloučky A-B nebo E-F mají větší délku než B-C a ostatní. To přece ve svém lidském zrakovém vnímání nepozorujeme.
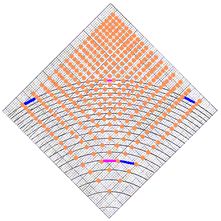
Obloučky různé délky
Nebo fialový oblouček, také je kratší než dva modré, na největší čtvrtkružnici.
Zdůvodnění - možnosti
a) Sousední body v našem světě jsou nahuštěné, navzájem vzdálené o minimální vzdálenost. Tu fyzika zavedla Planckovou konstantou 10-34. metru. Tedy 1034 bodů vytvoří délku 1 metr. Tento vliv lze dál promýšlet, i když nelinearita rozložení zůstane i nadále.
b) Dál jen ukázka, že rozlišování zrakových zážitků je složitou činností, kterou lidský mozek, ve své konstrukci, má mimořádně složitě zajištěnou.
Blindsight, doslovně vidění slepých, se zkoumá už půl století. Pro pochopení vztahu mezi mozkem a zrakovým vědomím (vím, že vidím) je blindsight důležitý tím, že ukazuje, jak zvířata i lidé, nevidomí proto, že mají poškozené zrakové oblasti mozku - oči, ale zrakové „nervy“ mají v pořádku -, se v některých situacích chovají, jako by slepí nebyli. Blindsight byl definován jako zpracování zrakové informace, které si zvíře nebo člověk neuvědomují. Lidé říkají, že nic nevidí - a nelžou -, nicméně jejich chování nebo chování jejich organismu vypovídá o tom, že jejich mozek zrakové informace přijímá a zpracovává. Přijaté zrakové informace si však neuvědomují, neproniknou do jejich vědomí. s. 74 Podobně jako může ložiskové poškození mozkové kůry způsobit poruchu rozlišování barev, může způsobit i poruchu rozlišování pohybů… Jakmile tito pacienti nalévají z konvice do šálků čaj, obvykle přelijí. Proud čaje vidí jako oblouk zamrzlé tekutiny. Jsou ohroženi při přecházení ulice - nerozlišují, že se blíží auto. Nejprve je spatří v dálce, vzápětí auto „vyskočí“ přímo před nimi. s.58
Je náročné studovat vizuální činnost mozku; oč náročnější je takovou záležitost uskutečnit. Dodnes si to mnozí lidé neuvědomují.
Obrovský zorný úhel, kterým disponujeme, nemůže zajišťovat zrak. Lidský mozek si periferní vidění do značné míry sám vymýšlí [Nic není, jak se zdá. Periferní vidění je z velké části jen optickou iluzí - Stanislav Mihulka, 10.12.2016].
Když si stoupnu ke zdi a nosem se jí dotýkám, vidím i pohyby rukou, hned vedle zdi. Přitom tyto vjemy nemůže oko zajistit. Toto je další téma, které zde už nebude rozvíjeno. Zda bereme zrakové zážitky jen z očí nebo zda jinak.
Zhodnocení
Bodový prostor je navázaný na zrakovou perspektivu. Tím se přibližuje posuzování světa v podobnosti s informatikou, s počítači. Zdrojem smyslových zážitků by mohla být nadřazená Informatika a nikoliv hmota.
* * *
Zdroj:
Speciální teorie informatická - Bohumír Tichánek. Vydalo roku 2023 nakl. Cyrrus Trade ISBN 978-80-7504-65 7-4
Já. O vztahu mozku, vědomí a sebeuvědomování - František Koukolík. Nakl. Karolinum, UK Praha 2003






