Článek
1. Prostor
Počínajíc teorií relativity se začalo pochybovat o samotném fyzikálním prostoru - má vlastnosti, nebo se jedná jen o vzdálenosti mezi kusy hmoty? Když jeho náplň - éter, byla tehdy odmítnuta.
Nyní předpokládám uměle vytvořený prostor, ve prospěch vnímajících vědomí. Prostor je tvořený rastrem. Tedy neviditelnou, nehmatnou mřížkou, působištěm pro výskyt informatických bodů. Tyto nám dávají vjemy hmoty.
O prostoru pojednává mnoho fyziků i laiků. Porůznu vybírám názory na prostor, matematický a fyzikální:
Prostor vyjadřuje vzájemné poziční vztahy jednotlivých předmětů a jejich částí
Prostor P je množství určitých prvků (to jest určitých ´věcí´)
Prostor je jakákoli neprázdná množina
Prostor - nejrůznější soubory všelijakých útvarů, jež jsou body takového prostoru
Prostor jest jen souhrn určitých vztahů na daném obsahu
Prostor chápe věda jako způsob rozmístění současně existujících objektů a čas je posloupností existence těchto neustále se měnících jevů
Prostor má vlastnosti: permitivitu, permeabilitu; dle jednoho ze známých názorů se tím potvrzuje, že prostor je.
2. Bodový prostor
Jsou důvody, proč hledat - za makrokosmem i mikrokosmem - oddělené body diskrétního (bodového) prostoru.
Mohou nás přibližovat k nalezení důvodu postulátů STR. Viz - konstanta c, její dodržování jistě souvisí s podstatou prostoru.
Přepočet diskrétních bodů nabízí alternativně zdůvodnit perspektivní vjemy lidského zraku. I když lidské vjemy podléhají různému šálení, jak známo.
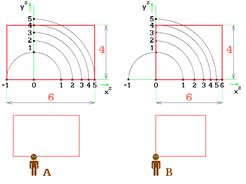
Vjemy zlatého řezu
Diskrétní přístupy sice fyzika odedávna zvažovala, ale přesto Max Planck sám byl překvapený, když roku 1900 výpočtem prokázal částicovou skladbu paprsků záření. A později podobně pro dalšího vědce, který prokázal částicové složení hmoty:
Rutherfordova skupina tušila, že Bohr možná objevil předpoklad pro vytvoření nového způsobu popisu přírody. Německá fyzikální elita v Göttingenu se však k tomu stavěla skepticky až odmítavě. Bohrovi to sdělil bratr Harald, který se krátce po své promoci dostal do nejvyšších sfér matematiky. Matematik Carl Runge prý dokonce vyslovil podezření, že se tento vysoce inteligentní mladík snad zbláznil.
Začít uvažovat, že kolem jádra krouží elektrony? Na zakřivené dráze přece svou energii vyzáří, takže rychle spadnou do jádra. A přesto Bohr odvážně určil podmínky:
• elektrony obíhají kolem jádra po předepsaných drahách.
• atom září jen při přeskoku mezi předepsanými drahami.
Model postihoval chování atomu i čárové spektrum jeho záření, a přesto tehdy nebyl snadno přijímaný.
Pročpak asi Runge chápal šílenost tohoto nápadu? Protože předepsané dráhy elektronů - jejich propočítání předem - to by bylo až příliš inteligentní provedení Vesmíru. Cesta zpět? Hledejme a až podle výsledků posuďme vznik Vesmíru. Spíš nestranně a opatrně, ale i odvážně.
*
Nahlédnu do znalých zdrojů. Ohledně relativistických vlastností hmoty Kuzněcov [9] citoval podiv Heisenberga:
Teorie relativity považuje za výchozí vztah zkrácení pohybujících se měřítek a zpomalení času v pohybujících se soustavách. Z hlediska kvantové teorie ale jsou měřítka i hodiny velmi složitá tělesa: Jsou sestrojeny, celkem vzato, z mnoha elementárních částic, působí na ně složitým způsobem různá silová pole a proto je nepochopitelné, proč právě jejich chování je popsáno zvlášť jednoduchým zákonem.
Heisenberg připomíná více působících vlivů na částice, jež jsou v konci podrobené jednotnému Lorentzově výsledku. Uvažuji - částice, ať se skládají z elementárních podčástic – informatických bodů. Proto na veškerou hmotu pak působí jednotný vliv – časové zpoždění.
Znalá fyzika sleduje nesrovnatelně složitější postupy než jenom počty. Zná leptony, hyperony, baryony, mezony pi a K, a mnoho dalších. Strunové teorie. Přesto, výše citovaná úvaha „o nepochopitelnosti“ může svědčit bodovým modelům, jež tyto články o STR a STI zde předkládají. Kdy zpomalování podléhají samotné body, jako základ hmotných částic. Podobně Leibnizovy monády a další.
Bodem zde rozumím informaci 1bitu o obsazení prostorové posice. Ta je informací buď obsazena, nebo ne.
*
Kuzněcov zvažuje diskrétní prostor:
Co je skutečně obtížné (a co není a nemohlo být Einsteinem uděláno), tj. najít mikroskopické procesy, které by vysvětlovaly vztah mezi prostorovými a časovými měřeními v soustavách, které se vzájemně pohybují. Ani nyní nemůžeme jednoznačným a spolehlivým způsobem ukázat, jak mikroskopická struktura látky vede ke vztahům Einsteinovy teorie relativity. Těmito vztahy se řídí všechny procesy v světě galaxií, planet, molekul a atomů. Je jim podřízeno chování elementárních částic v libovolně malých prostoročasových oblastech? To dosud nevíme. Předpoklad o diskrétnosti prostoročasu se zdá být přirozený už proto, že byl vyslovován v každé etapě rozvoje vědy.
*
Co se v technice objevilo později, kterým směrem šel vývoj? Je mnoho rozdílů mezi počátečními desetiletími 20. a potom 21. století. Například přechod od analogové k diskrétní sdělovací technice, dále zásadní vliv informatiky a i osvojení virtuální reality. Kdysi lidé teprve poznávali podstatu pohyblivého obrazu na plátně - připomíná se příběh, kdy diváci prchali ze sedadel, když se jim blížila promítaná černobílá lokomotiva. A to jela bez doprovodného zvuku; film byl němý.
Snad to něčím připomíná popletení z dob, kdy telefonní aparát byl zásadně kabelem připojený do ústředny a pak další kabel vedl ke zvolenému druhému účastníkovi. Jenže co když byl kabel překopnutý? Volající slyšel ve sluchátku vyzváněcí tón a nedal si vymluvit, že slyší zvonění u volaného účastníka. Ne, slyšel tón, který mu posílala ústředna do sluchátka, bez ohledu na nepřipojení druhého účastníka.
Něco dostávají lidé jako smyslové informace, ale je potřebné znát víc. Lze předvídat budoucnost, cestovat do minulosti? Tohle všechno pomáhá civilizaci přežít. aby ji nezničila kometa, která by měla dopadnout na Zemi.
Již několik desetiletí známe zdánlivou, uměle připravenou skutečnost, a to zásluhou počítačové techniky. Cestovatelka zajímavě popisuje i hodnotí virtuální zážitek z Ameriky [25].
I na další stránce Kuzněcov promýšlí diskrétní přístup k STR:
Proto je možné předpokládat, že ve svém dalším vývoji dospěje fyzika k nějakému kvantově atomistickému opodstatnění teorie relativity a že v takovém opodstatnění budou figurovat přirozené konstantní veličiny - minimální vzdálenosti a minimální časové intervaly.
Kvantové přístupy značí přístupy rozkouskované – na nejkratší úseky. Tomu zkouším přibližovat své modely, i když jen v nejjednodušších souvislostech.
Dávný český filosof Vorovka citoval, vyzdvihoval diskrétní prostor ve fyzice v myšlenkách tří velikánů:
Riemann připouští: ‚že by to skutečné, co je podkladem prostoru, tvořilo přetržitou množinu‘. ~ ~ ~ Weyl komentuje: ‚Snad jednou právě v této možnosti bude nalezena odpověď k problému prostoru.‘ ~ ~ ~ Dedekind: ‚Má-li prostor vůbec reálnou existenci, nemusí být proto ještě spojitým, nespočetné jeho vlastnosti zůstaly by týmiž, i kdyby byl přetržitým.‘
*
Znovu Kuzněcov [9]:
Koncem minulého (19.) století George Johnstone Stoney (1826 - 1911) přišel s myšlenkou o minimálních prostorových vzdálenostech 10 na minus 35 cm a minimálních časových intervalech 3·10 na mínus 45. s. Za padesát let poté V. Ambarcumjan a D. D. Ivaněnko vyslovili předpoklad, že v kvantovém světě mohou mít souřadnice pouze celočíselné hodnoty, pokud jsou vyjadřovány v jednotkách elementární délky. ~~~ Brzy potom však Heisenberg publikoval práci, v níž se hovořilo o minimálních prostorech a vzdálenostech. Heisenberg soudil, že elementární délka bude základem ohraničení kvantové mechaniky, podobně jako kvantová konstanta ohraničuje klasickou mechaniku. ~~~ Také N. S. Snyder a také M. Coish dospěli k představě, že v ultramalých měřítkách není prostor spojitý, ale diskrétní, to jest sestávající z jednotlivých jasně ohraničených bodů - buněk. Uvnitř takové buňky lze sice prostor nekonečně dělit, ale této dělitelnosti neodpovídá žádný reálný fyzikální proces. Můžeme si představit vzdálenosti menší než 10 na -13. cm a časy menší než 10 na -25. sekund (elementární trvání), ale těmto měřítkům nebudou odpovídat oblasti či časové intervaly fyzikálně navzájem odlišné. ~~~ Základní práce k dané problematice je Snyderova studie roku 1947. Prostorové souřadnice mohou mít jen diskrétní hodnoty: x, y, z = ±l, ±2·l, atd., kde „l“ je jistá elementární délka a nic nemůže být menší než ona.
*
Ve stejném směru:
Kvantová struktura prostoročasu ukazuje, že menší vzdálenosti než 10 na -33. cm a kratší časy než 10 na -43. s nemají význam, protože prostorové vztahy a časové relace zde vlivem kvantových fluktuací topologie ztrácí smysl.
V [11] přidává k odstavci z [10] poslední větu. Názor se dotýkal filosofie?
---. A to je poznatek svým významem přesahující rámec geometrodynamiky a dokonce i celé fyziky.
*
Ze 17. století - Leibnizovy monády vystihovaly posice (šachovnici), potřebné bodovému prostoru:
Leibniz tvrdí, že rozprostraněnost je výslednicí působení bezrozměrné dynamické substance, které roku 1697 nazval monádami. Monády nejsou geometrické body, vždyť ty předpokládají existenci prostoru, ale monády, dle Leibnizových slov, samy vytvářejí prostor.
*
Ještě dávnější učenec uvažoval nejen diskrétní prostor, ale i čas [13]. Takový názor nespojitého prostoru a času vede k neustálé obnově Vesmíru. Může jít o pulsaci.
Stanovení nejkratších dílů prostoru a času závisí na dalších vlivech, které už přesahují hledání jednoduchými mechanickými modely.
V arabské filosofické literatuře se projevilo atomistické učení o prostoru a času, které jak známo zavrhoval Aristoteles a v matematické formě Eudoxos a jejich stoupenci. Toto hledisko zastával a rozvíjel Abu´l - Hasan Alií ibn Isamá´íl al-Ašarí. Na základě učení o diskrétním charakteru času a pohybu, mutakallimisté dělali neodůvodněný indeterministický závěr, že v každém právě probíhajícím atomu času Alláh vždy znovu tvoří celý svět a tedy ve světě nemohou existovat žádné příčinné souvislosti. ~~~ Toto učení nezůstalo bez odezvy ani v matematice. Z hlediska mutakallimistů jsou dvě libovolné veličiny stejného druhu vždy souměřitelné a neexistují tedy iracionálně. Při rozpracování své obecné teorie proporcí se Chajjám o tomto pojetí zmiňuje a ačkoli ho nesdílí, nezavrhuje možnost vítězství matematického atomismu v budoucnosti a snad ani nepovažuje za vhodné ji zavrhnout.
Názor vždy nového tvoření světa sleduje časovou nespojitost, ačkoliv smysly nás přesvědčují o kontinuitě času. Dávný názor al-Ašarího vystihuje obrázek, který kvadratickou Pythagorovu větu (zde: 102 + 102 = u2) přemění v lineární rovnici: 10 + 10 = 20.
Perspektiva počítá s jinými čísly, dává jiné výsledky. Mám za to, že vystihuje sestrojení Vesmíru, kdežto konstrukčním výpočtům je nadále vhodný lineární prostor. Než se najde nadaný vědec, který…
u… délka úhlopříčky
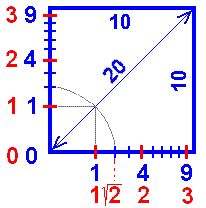
Čtverec cejchovaný Euklidovým a perspektivním měřítkem
A závěr géniův:
Nekonečnost a věčnost, tyto dva atributy Boží, nacházel také u prostoru a času, a proto si prostor představoval jako smyslové ústrojí Boží.
*
3. Váhání nad spojitým prostorem v matematice:
Na druhé straně se však dnes stále více ukazuje i to, že v myšlence kontinua je nějaká záhada, začínající budit dojem něčeho nezdravého. Prostě kontinuum začíná budit nedůvěru odborníků. Tito odborníci začínají volat po revizi všeho, co s kontinuem souvisí. Chtějí nahradit kontinuum něčím nespojitým, chtějí kvantovat matematiku nějak podobně, jako již předtím začali fyzikové kvantovat fyziku. Ozývají se další a další hlasy, požadující znovuprověření všeho, co bylo vybudováno na pojmu nekonečně malé veličiny, byť by to byly matematické vzorce a metody nesčetněkrát prověřené praxí. Tito odborníci ukázali, že lze stejné vzorce odvodit i z představ „kvantované“ matematiky, pracující nikoli s veličinami nekonečně malými, nýbrž velmi malými.
Nutný krok, který učinil Newton od veličin konečných k nekonečně malým, je založen na vážném předpokladu. Ten byl v době Newtonově zcela přijatelný, dnes však jeho oprávněnost není již tak jistá. Očekáváme totiž, že při přechodu k nekonečně malým rozměrům délkovým i časovým nedojde k podstatným podstatným změnám ve vlastnostech věcí. Předpokládáme, že měřítka i hodiny měří plynule, spojitě, všechny vzdálenosti a časové úseky od nekonečně malých až k běžným. Někteří fyzikové se dnes domnívají, že tento předpoklad není oprávněný. Mají-li pravdu, pak to může znamenat, že ani pouhé přemísťování není proces zcela spojitý, plynulý; v každém případě jejich pochybnosti vedou k představě, že „pouhý“ mechanický pohyb je děj ve skutečnosti složitý.
*
4. Několik názorových přiblížení k virtuální realitě
´metafyzický realismus´ jako forma světového názoru. Reálný svět není, tvoří se ve fantazii subjektu. ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ Obsah odpovídající novému pohledu na svět nepotřebuje mlhavé alegorie, náhodná pozorování a sblížení ani řečnické výkřiky a hromadění starých textů, ale jasné obrazy načerpané z bezprostředních dojmů a technické zkušenosti.
Hegel nemohl přijmout některé pozitivní momenty Kantovy filosofie mimo jiné i proto, že odmítl jeho výchozí tezi, dle níž objektivní realita (věci o sobě) působí na naši smyslovost a tím vyvolává počitky čili „materii“ vědění.
*
Neopomenu čisté dětské vnímání prostoru, ostatně i Einstein z takového vycházel. Jan Evangelista Purkyně:
Jeli jsme přes Veltrusy, kde jest dosavád veliký přívoz. Vůz vjel na prám, my vstoupili a já myslel, že je to most, neboť zdálo se, že stojí, a já sem a tam se procházel, jen mně podivno bylo, že okolní břehy se pohybovaly. Konečně přistál prám na protější břeh, my vystoupili a já nejinak myslel, než že jsem po mostě se procházel.
*
5. Zhodnocení
Užité výpisy sledují možnost, že náš Vesmír je založený bodovým prostorem. Takové skutečnosti dbají modely této práce.
Matematika je nám rozhodujícím vědeckým nástrojem. Jenže ona dosud náš svět popisuje jen přibližně, a to vlivem iracionalit. Ty přísluší Euklidově prostoru. Naproti tomu se nabízí výhoda užití prostoru bodového. Snaha pro úplnou přesnost posléze směřuje k převodu do perspektivního prostoru – s vynecháním prostoru Euklidova nebo i zakřivených.
Matematika je už mnohem dál než bylo poznání dávných tisíciletí.
Skládá-li se úsečka z nekonečného množství bodů, pak jiná větší úsečka musí obsahovat větší počet bodů, než je nekonečno.
Ostatně, pozor na dávné počítání bytostí, jež se mají vměstnat na špičku jehly. A když jsme u andělů, pak uzavřu biblickými posudky:
´To spíše projde velbloud uchem jehly než boháč do Božího království.´ - Bible 21. století, Evangelium podle Lukáše. ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ Novější bádání však navrhuje číst v řeckém textu kamilos (tj. lano) místo kamélos (tj. velbloud). I v arabštině je možné číst džamal, velbloud, anebo džumal, lano; tak navrhovali již někteří staří muslimští komentátoři, protože se lépe hodí do textu. LXXXV Súra 7, verš 38/40, s. 719
Zdroje:
[1] LIDI aneb Většina národů má za to, že je úplně jiná než většina národů - Milena Holcová. Nakl. Šalvar, Brno 2001, s. 154 - 157… výňatek z knihy
[2] Umění vidět v matematice - František Kuřina. SPN, Praha 1989, s. 111
[3] Vyšší škola technického kreslení - Kochman, Švejda, Klepš. Práce, Praha 1967, s. 15
[4] Kde žijeme? Geometrický podklad dnešního názoru na prostor - Karel Havlíček. JČMF, Praha 1949, s. 43
[5] Cesty moderní matematiky - Karel Havlíček a kolektiv. Horizont, Praha 1976, s. 79
[6] Kantova filosofie ve svých vztazích k vědám exaktním - Karel Vorovka. JČMF, Praha 1924, s. 93, s. 106, s. 111
[7] SOS Rozhovory o budoucnosti - Vlastimil Halaxa. Masarykova univerzita, Brno 1993, s. 6
[8] Převratné objevy fyziky. Od Galileiho k Lise Meitnerové - Thomas Bührke. Academia 1999. (Orig. 1997), s. 158
[9] Einstein - život, smrt, nesmrtelnost - B. G. Kuzněcov. SPN, Praha 1984, s. 259, s. 264
[10] Gravitace, černé díry a fyzika časoprostoru - Vojtěch Ullmann. ČSAV, Ostrava 1990, s. 256
[11] Unitární teorie pole a kvantová gravitace.htm - Vojtěch Ullmann
[12] Od Galilea po Einsteina - B. G. Kuzněcov. Pravda, Bratislava 1975. (Orig. Nauka, Moskva 1966), s. 191
[13] Dějiny matematiky ve středověku - A. P. Juškevič. Academia, Praha 1977, s. 290
[14] Kde začíná budoucnost - Jiří Mrázek a kol. Naše vojsko, Praha 1989, s. 366
[15] Od fyziky k filosofii - Ivan Úlehla. Orbis, Praha 1963, s. 13
[16] Filosofické otázky současné fyziky - V. S. Gott. Orbis, Praha 1976, s. 116
[17] Kantova filosofie a současnost - Drobnickij a kolektiv. Svoboda, Praha 1981, s.11
[18] Nitky z mého života - Jan Evangelista Purkyně. Odeon, Praha 1987, s. 94
[19.a] Evangelium podle Lukáše. Bible, překlad 21. století. Vyd. BIBLION, z. s., 2021
[19.b] Korán - překlad Ivan Hrbek. Odeon, Praha 1991, s. 719






