Článek
Úvod
Znalý učitel tehdy posoudil výstižně – ovšem uvažoval v samozřejmém paradigmatu spojitého prostoru a času. Hlubší poznání, provozované v ošidné Máji, nejspíš dál už nemá naději. Neprohlédne příčinu zpomalování času, jež ve 20. století ověřila technika s vědou více způsoby.
K posuzování vlastností času jej nejprve dělím na úseky – kvanta. Diskontinuita. Však nejkratší Planckův čas je v kvantové fyzice k tomu nachystaný: 5,39121.10-44 s. Vypočítaný to zlomek sekundy. K tomu délka: 1,61624.10-35 metru.
Hlavní problém tohoto postupu mi připadá v tom, že vyžaduje Inteligenci za Vesmírem. Určitého Konstruktéra. A to stále ještě není dnešní civilizaci vhod. Pochopitelně, svět svůj původ sám od sebe neodkrývá, aby jeho umělé vytvoření nebylo snadno k rozpoznání. Nýbrž si na to musí civilizace přijít sama. Jistě obětavou prací ušlechtilých vědců - objevitelů. Biologů? Píše se, že buňka živočichů nemohla vzniknout nějakým postupným výběrem, nýbrž musela se objevit hotová, naráz.
Přetržitý čas a prostor do perspektivy
Bod hmoty posuzuji jako informaci 1 bitu o obsazení posice. V diskrétním prostoru je všechna hmota registrována, když každý její bod je umístěný v určité posici rastru. Užívají se pouze pravoúhlé přesuny, přeskoky o 1 posici. Úhlopříčný pohyb bodů mezi dvěma posicemi ať není umožněn.
V dalším informace přepočítává vesmírný Procesor do geometrie perspektivního prostoru, do zrakového vnímání. Hmotu neuvažuji – sleduji rovnou lidské zážitky hmoty, která není.
Příčina - body z diskrétního prostoru do Euklidova prostoru přepočítat nelze. Vkládám zde diagram, vzdálenost 4 od začátku souřadnic pro bod P je v obou obrázcích dodržena, ale souřadnice nikoliv. Přitom u perspektivního zobrazení to lze. Vybral jsem nadějnou sestavu pro hledání: diskrétně + perspektivně.
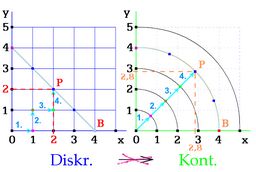
Převod bodu P z diskrétního do Euklidova prostoru nemá řešení
Někteří lidé chápou po tisíce let, že u zážitků hmoty nutno váhat: co je za nimi? Už ve starověku Platón popisoval stíny na stěně, promýšlel takto život ve virtuální realitě. V průběhu 20. století se tento pojem stále víc vyjasňoval i přibližoval.
Ve 2D prostoru má posice kolem sebe 4 sousední posice, jedině do nich může bod přeskočit. V tomto nejzákladnějším prvotním popisu.
Body ať se přesunují do sousední posice vždy jen na povel. Hodinový signál hypotetického vesmírného taktovacího Zdroje opakuje své pulsy. Nabízí přeskok každých 10-43 sekundy, (zjednodušený údaj), podle Planckova času. Pak 1 sekundu vytvoří 1043 pulsů.
V jednom pulsu bod neuskuteční víc přesunů; vykoná buďto jediný nebo žádný přeskok z posice do sousední posice. Pulsace diskrétního světa takto podmiňuje jevy spojitého perspektivního časoprostoru. Pokud bod přeskakuje v každém dalším pulsu Zdroje, pak letí rychlostí světla. Dodržování konstantní rychlosti fotonů, v důsledku činnosti Zdroje, mi připadá důvěryhodné. Setrvačností se přece nepohybují.
V diskrétním prostoru zavádím čas diskrétní, skokový. Přibývá v pulsech, a není to náš čas v sekundách. Pulsy nejsou naší jednotkou času, jednoduchý způsob přepočtu uvedu později.
Kosmonaut
Zdroj vytváří pulsy, které značím PE. Pokud je puls příčinou přesunu bodu do sousední posice, označuji ho jako délkový (pohybový) PL. Pokud nebyl využitý, je to puls časový PT. Je to jednoduchý nápad, snad právě jednoduchost je jeho předností.
Kosmonaut ať letí těsně podsvětelnou rychlostí. Jeho hmota přeskakuje vždy do dalších sousedních posic opakovaně, další a další zdrojové pulsy PE stále využívá jako PL. Když chce začít konat pohyb ze své vůle, nutno čekat, než se konečně objeví pulsy PT, nevyužité pro přímočarý pohyb PL.
Tehdy se bod v posici pohne libovolným směrem, do kterékoliv ze sousedních posic, jak vůle kosmonauta vybere. Například ve směru letu korábu a přemění PE na PL. Zajisté teprve obrovský počet PE dovolí člověku činit jeho zpomalený pohyb. Zpomalený, oproti stavu na Zeměkouli.
K pohybu ze své vůle může kosmonaut využít jen těch pulsů, které koráb s jeho tělem k setrvačnému letu nevyužívá. Přitom však na korábu žádné zpoždění nezjišťují. Ani svými smysly s myšlením, závislým na hmotě, ani hodinami. Jak nás už dávno naučila Einsteinova nauka.
Zde známé poznatky doplňuji úvahami o pulsaci.
Pro naše běžné pomalé rychlosti pohybu vyplývá jediná možná rychlost pohybu. Pohybujeme se výhradně rychlostí světla „c“. Tedy Zdroj tvoří PE, obrovské množství jich zůstane nevyužitých PT, a jen nepatrné množství PL jich slouží k našemu pomalému pohybu. Přeskoky bodu z pozice do pozice nechť se dějí rychlostí světla.
*
Nabízím grafické fázované zobrazení, v 8 pulsech. Postava je bez pohybu, stoupá po časové ose souměrného diagramu.
Kosmoplán užije každý 2. PE k pohybu, kresleno vodorovně. Kdežto když se geometrickým prostorem nepohybuje, PE změní v PT, tehdy by mu hodiny zaznamenaly další sekundu, v tom pulsu PT. Pro názornost jsem v naukovém obrázku zvolil 1 PT = 1 s, zatímco ve skutečnosti lze pro Zemi chápat 1 PT = 10-43 s.
Foton si letí svou plnou rychlostí. Všechny tři objekty stále zůstávají na společné časoprostorové kružnici, vždy další, větší. Mají současnost. Kosmonaut v kosmoplánu vzpomíná, co asi dělá stromek, který zasadil - dnes už to bude vzrostlý strom. Takže čas plyne kosmonautovi a stromu jinou rychlostí, ale mají současnost. Tohle nabízí a dovoluje tato informatická nauka, kdežto STR současnost nezná.
*
Zatímco první fázovaný obrázek ukazoval časoprostor, druhý ukazuje pohyb korábů 1D prostorem.
Druhý fázovaný obrázek obsahuje tři kosmické koráby. Horní neodstartoval, druhý a třetí letí setrvačností a liší se svými rychlostmi. Zobrazení má 11 fází, oživuje ho 10 PE. Koráb, co zůstal na startu bez pohybu, rezaví nejrychleji. Všechny PE si mění v PT. Na jeho palubě běží čas nejrychleji, oproti dvěma ostatním korábům. Spodní koráb letí největší rychlostí, na 1 PT se zastaví až po mnoha PE, které měnil na PL. V korábu jsou uváděná čísla, která značí, kolik PT koráb prožil.
Mion
Popíšu známý fyzikální případ letící částice. Vlétne obrovskou rychlostí do ovzduší Země. Srazí se s jádrem atomu v ovzduší, ve výšce desítek kilometrů. Následně vznikne nová částice - mion. Její životnost je krátká, brzo se rozpadne. Měl by doletět jen 600 metrů, a pak by se mion rozpadl na elektron a dvě neutrina. Avšak ve skutečnosti letí mnoho kilometrů, a i dopadne na povrch Země.
Je to překvapivý jev, když vydrží déle, než se rozpadne - opožděně ve srovnání s miony, které se vyskytují na Zemi bez velké rychlosti. STR souvislost vysvětluje s užitím změněného času a délky.
Pulsní časoprostor STI zkouší podrobněji, po pulsech. Rozděluje trvání existence částice na okamžiky – pulsy pohybové PL a časové PT. Miony v pulsech
- PL - body mionu přeskakují do sousedních posicí a tehdy se ani nemění rozložení mnoha hypotetických informačních bodů, jimiž je tvořen. Při přeskocích jim nenabíhá čas, a tehdy se mion nemění, nestárne. Proto doletí níž, k povrchu Země.
- PT – podle rychlosti letu k Zemi se objevují pulsy PE, nevyužité k přímočarému pohybu. Tehdy, během PT, se informatické body mionu přeskupují, mion stárne.
Kruhový pohyb kotouče
Nejprve sdělení, o co se jedná. Kotouč se otáčí okolo své osy a má přitom neskutečnou podsvětelnou rychlost. Einstein tyto pokusy, které neuskutečníme, často používal a nazýval je myšlenkovými.
Známé vysvětlení, které dává Speciální teorie relativity, STR. Ve velké rychlosti se hmota smršťuje. Pro kotouč to znamená zmenšení, zkrácení jeho obvodu. Právě hmota na obvodu, dál od středu otáčení, má větší rychlost. Kdežto hmota uvnitř kotouče, blíž ose otáčení, vlivem své menší točivé rychlosti se tolik nezkracuje. Paradox spojitého prostoru – vnitřek kotouče má strpět zkrácení vnějších obvodových částí kotouče. Rozdrcení jeho vnitřku! To je názor, jenž určila speciální teorie relativity - rychlost otáčení kotouče v podsvětelné rychlosti má vliv na jeho soudržnost.
*
Konkrétní úryvek s Einsteinovými názory příklad upřesní:
Ke smršťování obvodu kotouče, při nejvyšších rychlostech, cituje životopiscova kniha [4]:
Rádius se však s ohledem na pozorovatele ve středu nepohybuje, takže délka zůstává stejná, ať již disk rotuje nebo stojí v klidu. Znamená to, že Euklidova rovnice nemůže platit ve všech případech. Obvod rotujícího disku je kratší než obvod téhož disku, který se nachází v klidu.
Euklidovou rovnicí se rozumí výpočet obvodu kružnice, jenž užívá Ludolfova čísla π = O/d. Stav se smršťováním kotouče je trochu víc nesrozumitelný. Obvod se má smršťovat, hmota - zkracovat, avšak pozorovatel ve středu by sledoval neměnný poloměr. Takže, při vší úctě, tuším vnitřní rozpor těchto dvou souvislostí. Obávám se, že matematika zde převládá nad fyzikou. Že tohle už přesahuje virtuální realitu.
Dále Einsteinův popis [5]:
Měří-li tedy pozorovatel nejprve obvod kotouče, potom jeho průměr svým měřítkem a dělí-li potom oba tyto výsledky měření, nevyjde podíl známé číslo π = 3,14…, nýbrž větší číslo, zatímco na kotouči klidném vzhledem ke K by musilo přesně vyjít π.
Úryvky popisují změny délky obvodu při otáčení. Vnitřní body kotouče, o menší obvodové rychlosti, relativisticky mění svůj obvod méně intenzivně. Tak vysvětluje speciální teorie relativity ve spojitém prostoru.
Vložím cvičení – výpočet rychlosti, pro nás neskutečné:
Kotouč má poloměr 1 metr. Jeho úhlová rychlost ať činí např. pootočení o 10° za 1 nanosekundu.
Bod na obvodu se otočí za t = 360°/10° = 36 ns.
Obvod kotouče O = 2πr, vychází asi 6 metrů. Bod na obvodu kotouče má rychlost
v = O / t = 6 m / (36 · 10-9 s) = 166.000.000 m/s = 166.000 km/s. Předpokládám vypočtené rychlosti, že její relativistické souvislosti nejsou zanedbatelné. Vlivem rozdílných úhlových rychlostí okrajová hmota kotouče rozdrtí jeho vnitřek, což je známý relativistický příklad ke tříbení mozkové činnosti.
I když se v posledních desetiletích názor o změnách délky opouští, snad má jít jen o vjemy pozorovatele - což Einstein nevěděl. Citoval jsem dvěma odstavci ve Fyzika 5, které ovšem nesdělují totožně. Ostatně publikaci brněnských vědců rád vzpomínám: „STR není tedy jednou z mnoha fyzikálních teorií, ale spíše programem pro další rozvoj fyziky, jehož naplňování není dosud u konce.“
*
Nyní jinak, moje soukromá Speciální teorie informatická, STI. Okrajové, obvodové body kotouče stárnou pomaleji než vnitřní hmota, která je v pomalejším pohybu.
Odbočím - Zdroj buďto hmotu vytváří svými „éterovými“ pulsy PE, 1043 krát za sekundu. Anebo hmota by zůstala absolutně bez pohybu, kdyby PE Zdroje ustaly, a toto je mi naznačeno jako důvěryhodnější. Kampak bychom se dostali bez fantazie? Vracím se:
Mnoho Zdrojových PE bude obvodem kotouče spotřebováno na pohyb, na PL. Pak na obvodě zbývá málo časových pulsů PT na různé pohyby, opět vzpomenu rezavění. Vnitřek kotouče se točí pomaleji, má menší obvodovou rychlost při stejné rychlosti úhlové, takže víc zdrojových PE se mění na PT. Ty mohou být využity k pohybu bodů - přeměn na PL, a to například pro okysličování. Žádné drcení vnitřku kotouče zde neuvažuji.
STI: Obvod kotouče rotací nemění svůj rozměr, ale hmota, při obvodu kotouče, stárne pomaleji než vnitřní hmota.
Pro představu - znovu alespoň odkaz na statický obrázek, pomůcku k představě, jak se může otáčet kolečko v této diskrétně-perspektivní nauce. V diskrétním prostoru ať body čtverce postupují, tak říkajíc „kolují“ obvodem čtverce. Všechny na povel PE. A v našem „hmotném“ světě točivý pohyb kulatého kotouče chápeme.
Zeměkoule
Naše Zeměkoule, nechť má velmi malou rychlost setrvačného pohybu, když se přesunuje posicemi diskrétního prostoru. Proto mají pozemšťané možnost přesunu ve většině pulsů, které Zdroj vytváří. Procházíme životem vlastními pohyby rychleji než ti na podsvětelném kosmickém korábu; žádný dlouhotrvající translační pohyb nám nebrání, abychom využívali k zamýšleným pohybům nabídku skoro všech opakovaných pulsů Zdroje. Stárneme rychleji.
Na Zemi se hmota pohybuje pomalu; proto většina zdrojových pulsů, nabídnutých k pohybu, zůstává nevyužitá.
Zdroje:
[1] Speciální teorie informatická - Bohumír Tichánek. Vydalo roku 2023 nakl. Cyrrus Trade ISBN 978-80-7504-65 7-4
[2] Kvantový časoprostor - Bohumír Tichánek
[3] Fyzika V. Speciální teorie relativity a to se souměrným diagramem - Bohumír Tichánek
[4] Einstein v Berlíně - Thomas Levenson. Práh, Praha 2004, s. 97. (Orig. 2003)
[5] Teorie relativity - Albert Einstein. VUTIUM - VUT, Brno 2005, s. 139
[6] Základy teorie relativity - Novotný, Jan - Jurmanová, Jana - Geršl, Jan - Svobodová, Marta. Masarykova univerzita, Brno






