Článek
Úvod
Nevysvětlíme mořské rybě, co je oheň. V moři ani nezná důkladné teplotní změny svého prostředí, jaké našemu světu poskytuje počasí. Tohle jí vysvětlit by bylo ještě obtížnější, než abychom my pochopili podstatu 4D prostoru – jakým způsobem má rozmístěnou svou hmotu.
Ať se naše civilizace dočká své vzdálené budoucnosti. Pak může být, že velkou část svých aktivit schová pod zem, do skal a možná i do prostor na dně oceánů. Lépe chráněná před tajfuny, a i dopady těles ze Sluneční soustavy.
Dnes bychom si však neradi představovali vzdálení od živé přírody. Anebo - její obnovení v jiných prostorech a podmínkách by bylo skvěle zvládnuto…
Myslitel
Úplným základem výsledků Alberta Einsteina byly smyslové představy. Až následně je matematicky zpracovával – k výpočtům časů či gravitace v teorii relativity, k vysvětlení fotoefektu. Pochopitelně bez matematiky by jeho přínos nevznikl, až ten rozhodl.
Zatímco nejnovější životopisy zevrubně pátrají po stopách původu jeho teorií v jeho soukromém životě, fyzikové si stále jasněji uvědomují, že Einsteinovy teorie nevycházejí z tajemných matematických výpočtů (natož z jeho milostného života), ale z jednoduchých a elegantních fyzikálních představ.
4D prostor
Před 150 lety zasáhla lidstvo myšlenka čtyřrozměrného (4D) prostoru. Zpracovávali jej porůznu Lagrange, Mobius, Grassmann, Hamilton, Schläfli, Hinton, Abbott, Steiner, Minkowski a další. Básnili o něm spisovatelé, prostě zajímavost z matematiky se přesunula i do uvažování. Asi jako nyní v jiné záležitosti - k existenci našich mimozemšťanů.
Matematicky je nadprostor (3+1)D důkladně zpracovaný. Jenže my nežijeme v matematice, nýbrž ve smyslových zážitcích – a to je jiná. Dál bývá potřebné jejich následné rozumové zpracovávání. Například - aby padalo kamení z nebe, je to vůbec možné? V 18. století o tom věda pochybovala.
Svět si můžeme představovat jako geometrickou omáčku. Takový přístup nám nabízí každodenní zrakový vjem spojitého prostoru.
Úsečka je v něm sestavená z pohádkových, nekonečně malých bodů; a stejně tak blízkých. Někteří by soudili, že rovnoběžky jdou až do nekonečna, kde se nakonec sdruží – jenže, pokračovat do nekonečna znamená, že to nikdy nenastane.
Spojitý prostor nám ztěžuje vyhledání, jakým způsobem byl sám vytvořený. Vzniklý ve prospěch vnímajícího vědomí, které předtím žádný prostor nemělo. Spojitost víc vyhovuje touze po rozprávkově nepoznatelném a neřádném. Avšak hned za spojitostí se nachází směr k takovému Stvořiteli, který dbá pořádku, jedná zákonitě a i nalezitelně. Vždyť, je-li zdrojem poznání věda:
Vesmír vypadá, jako by byl navržen čistým matematikem.
Získat představy o geometrických vyšších rozměrech, k tomu je třeba dbát mechanických modelů prostoru. Jaké i tvořivý geniální fyzik nejprve promýšlel, coby své smyslové představy – ovšem na tom se nezastavil. Pokračoval ke světovým úspěchům výpočetně.
Mějme na talíři rýži. Zrní, buňky ať tvoří prostor, namísto omáčky. Oddělené pozice pro body dovolí vznikat útvarům ve vybraném počtu směrů – geometrických rozměrů. V nich všechny body můžeme mít spočítané, včetně posledního. Bodový, diskrétní prostor nabízí sestavování libovolně rozměrných prostorů, ve prospěch smyslového posouzení. Takové počty snad potom přiblíží i příčinu, proč se zpomaluje čas hmotě v pohybu?
Krychle
Krychli si snadno představíme jako těleso složené z naskládaných rovin. Čtverce, narovnané na sobě, vytvoří krychli. Náš zrak, s 2D sítnicí, vidí povrch krychle - čtverec, nebo jiné obrazce podle současného natočení tělesa.
Vrstvy 2D skla
Pokud by však byly naskládané, na sobě, průhledné skleněné tabulky (jakoby 2D vrstvy), pak bychom viděli i do hloubky skleněné krychle. Zahlédli bychom například barevné kaňky na vnitřních tabulkách.
Krychle 4D
Sestava krychlí vytvoří 4D krychli. Každá použitá krychle má ve 4D prostoru svůj 3D prostor.
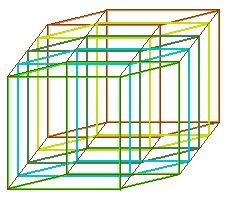
4D krychle je tvořená krychlemi, které se prostupují - hodnocení z 3D prostoru
Ve čtvrtém prostorovém rozměru má každý 3D objem samostatnou existenci, a přitom každý bod objemu sousedí s odpovídajícími body obou sousedních objemů.
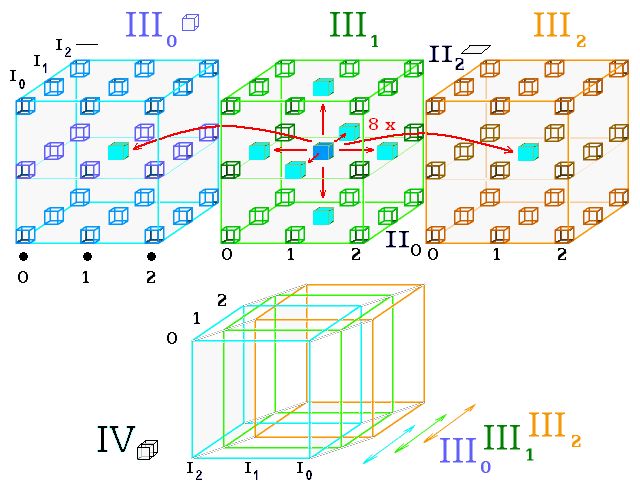
Ve 4D krychli má bod 8 bodů sousedních
Znovu:
Hypotetický 4D prostor je složený ze sousedních objemů. Hodnotím je jako posunuté vždy jen o malý kousek. To se pak svými objemy prostupují – dle našeho hodnocení? Ne, ony objemy existují každý sám pro sebe, neprostupují se ← v odkazu se kreslí sled krychlí, a nakonec se zdůrazní obrysy. Až to je obvyklé zobrazení 4D krychle.
Úhlopříčky
Postupné zobrazení všech úhlopříček 4D krychle ← nejprve ve čtverci, pak v krychli a ve 4D krychli (obrázky tvořeny kdysi ještě v *.pcx)
*
Úhlopříčka tělesová (3) sledovaná v nejbližší krychli, která je součástí 4D krychle. A také čtyřtělesová úhlopříčka (4) ve 4D krychli.
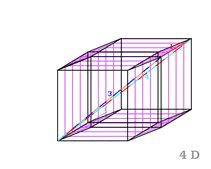
Úhlopříčka 3D tělesová (3) a čtyřtělesová (4)
*
Úhlopříčky ve 5D krychli:
čtyřtělesová (4) přes 4D krychli a pětitělesová (5) přes 5D krychli.
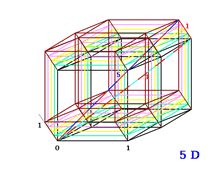
Úhlopříčka 4D (4) ve 4D krychli a 5D (5) v 5D krychli
*
Soubor „Úhlopříčky různých prostorů“ obsahuje „Zdůvodnění promítnutých obrazců -Výskyt úhlopříček - Délky úhlopříček“. Celkem 71 obrázků ve 3 obrázkových souborech (*.gif), ovšem většina obrázků je nachystána i k samostatnému zhlédnutí.
*

Rovnice a vjemy
Vidění v našem 3D prostoru
Objekt a oko jsou nakreslené spojité, kdežto níž jsou bodové. Sítnice má tvar čtverce. Objekt 3D promítá na sítnici (2D) jen svůj povrch. Tudíž zelenou a fialovou kaňku oko uvidí, kdežto modrá kaňka zůstává skrytá uvnitř 3D tělesa. Objekt září jen paprsky dvou barev.
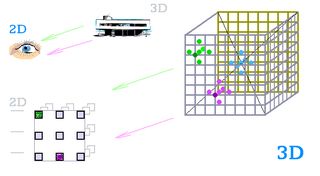
Oko a viděný objekt, oba jsou 3D. Spojité a bodové provedení
Vidění ve 4D prostoru
Oči člověka tohoto 4D nadprostoru, Čtveráka, předkládají 3D „obrazy“. Vidí, vnímá vše v hloubce objemu. Kdežto my – o jeden rozměr méně – vnímáme jen plošný otisk 3D okolí, tedy 2D obrazy.
Čtyřrozměrný Čtverák hledí na 4D krychli. Sleduje celý objem první ze všech krychlí, tedy všechny body jejího vnitřku, té nejbližší z celé řady, jež tvoří 4D krychli. Celé jeho oko (vlevo dole) je tvořeno 3D objemy, a až ta poslední 3D krychle znamená 3D sítnici.
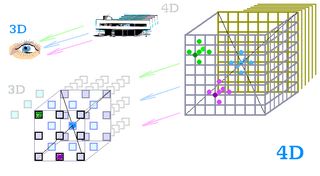
Oko a viděný objekt, oba jsou 4D. Spojité a bodové provedení
Vrstvy 3D skla
U nás, ve 3D světě, nevytvoříme 4D prostor. Ovšem – přece něco zkusím. Představme si řadu skleněných průhledných krychlí, navíc ať se prostupují. Tak, jakoby naši šikovní skláři vyrobili 3D sestavu, kterou vídáme jako průmět 4D krychle na 2D obrázek.
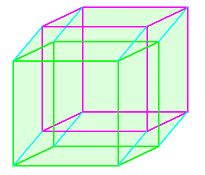
4D krychle spojitý pohled
Představuji si zrakový zážitek tvora 4D prostoru tak, že v řadě objemů vidí stále dál, skrz jednotlivé objemy. Například v každém z objemů se uprostřed nachází jedna koule, a taková řada mnoha koulí, navazujících velikostí od nejmenších po největší a pak rozměrově zpět, vytvoří 4D kouli.
Podobně jako v našem 3D prostoru můžeme chápat kouli jako objem, po 2D vrstvách sestavený z kruhů – od nejmenšího k největšímu a pak jsou zase zmenšované.
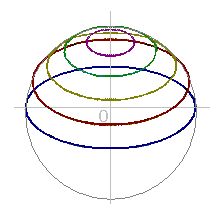
Koule sestavená z vrstev kruhů
Připomenu, že my máme 2D vidění, když žijeme ve 3D prostoru. Vnímáme skrz plochu oční sítnice. Trojrozměrné objekty předávají do 2D sítnice zážitky, například – k nám přivrácený povrch domku na blízku, a kolem něho – vzdálený les.
Ve 4D prostoru by měl tvor 3D vidění, sítnicí je krychle vlevo. Vnímal by celý objem III0 toho prvního ze všech objemů III0– III3, jež mu tvoří sledovaný 4D prostor. První z 3D objemů není celý zaplněný hmotou (zelené body), takže dál by se Čtverákův 3D vjem v 3D sítnici doplňoval zářením z hmoty vzdálenějších objemů III1 a III2. Ze III1 by do sítnice pronikl jediný modrý bod, ostatní by zadržel objem III0 pozorovaného 4D objektu (III0 – III2).
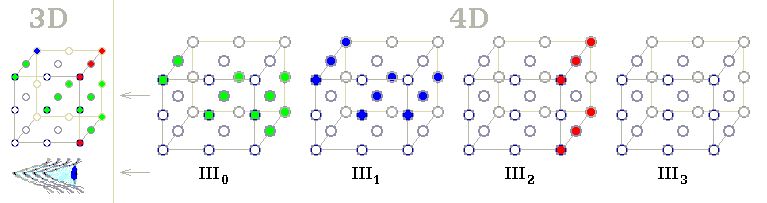
4D vidění, 3D sítnice
Znovu. Čtverák zásadně vidí vše vevnitř prvního nastaveného objemu III0, my jen výjimečně – ve skle. Když však první objem není Čtverákovi hmotou zcela zaplněný, pak mu vzniká zážitek i ze vzdálenějších objemů. Tak posuzuji 4D vidění. Uplatní se tyto přístupy v budoucí počítačové virtuální realitě čtyřrozměrného prostoru?
Obrys 4D koule
Obrysem kruhu je kružnice. Otáčení kruhu nám zobrazuje elipsu proměnné velikosti, až i úsečku – zvolíme-li k otáčení vhodnou osu. Perspektiva však zkresluje tvar elipsy vůči pozorovateli.
Obrysem koule je také kružnice, ovšem otáčením koule se její obrys nemění.
Vznik koule si lze představit v následku naskládání kruhů od nejmenšího k největšímu a zase nazpět. Viděný povrch koule pak tvoří obvody kruhů. Ovšem sestava z kruhů je jen myšlená. Hledí-li pozorovatel na kouli z kterékoliv strany, ony myšlené kruhy může znovu vrstvit – vždy směrem od sebe pryč.
Obrysem 4D koule je také jen kružnice. 4D koule by vznikla naskládáním koulí od nejmenší k největší a zase zpět. Byly by snad nakládané jedna za druhou? Ne, navzájem by se sousedky pronikaly, posunuté jen o nepatrný kousek. V mém pokusu, v obrázku jsou koule (postupně fialová, zelená, šedá, hnědá a modrá) deformované v elipsoidy. Obdobně jako na obrázku koule, umístěném výše, kde ji tvořily elipsy – vzniklé šikmým pohledem na kružnice.
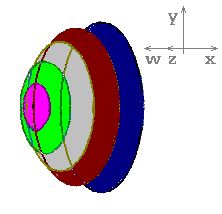
4D koule, spojitý pohled
Smysl přemítání o prostoru
Podstatou životního zážitku bývá vnímání hmoty s prostorem, s jejím ovlivňováním. Nejjednodušším způsobem zobrazuji 4D prostor s tělesy a tím zkouším posoudit, jakým promyšleným způsobem se asi vytváří náš 3D svět. Mechanické modely – obrázky, uvažované z oddělených bodů, přibližují výsledky našemu chápání.
Ve prospěch 4D představy vysokoškolský učitel někdy jen naznačí sousední objemy na obrázku, přesnější mechanické modely však netvoří.
Naopak vycházet ze spojitého prostoru, s jeho nepřesnými – bezvýslednými – iracionálními výpočty, například Pythagorovou větou? To mohla sledovat věta dávného filosofa:
Žádné náboženské vyznání nehřešilo zneužíváním metafyzických výrazů tolik jako matematika.
Vše v dávnověku sděleno a zapsáno? Lidé se snad ani nemají pokoušet zjišťovat, jak byl vlastně náš svět vyroben? Máme ho jen popisovat? To není dost. Byl vyroben příkazem? Jako když malé dítě řekne – dej mně to! A už to má.
Představme si jazykovědce, kteří by 98 % svého úsilí věnovali výpočtům. Zajímalo by je, jaký je průměrný počet hlásek ve slově, kolik slov má průměrně věta, které písmeno je ve slově nejčastěji první, které poslední. Které dvojice písmen se nejčastěji sdružují. A tak dál. S počítači by to byla zajímavá práce. Jenže přece jsou důležitější jiné souvislosti – laicky odhaduji – jaký byl vývoj jazyka v minulosti, jak asi do budoucnosti, jak vznikaly odlišnosti od příbuzných jazyků, a další, mně nepředstavitelné úkoly.
Podobně nezdůrazňují matematiku tvůrci ani v hudbě, ani v medicíně.
Kdežto fyzika staví víc dopředu počítání a upozaďuje mechanické modely. Dosáhla sice kolosálních úspěchů, ovšem věta „fyzika jako geometrie“ byla důležitými vědci vyslovena už dávno. Žijeme ve hmotě; její matematický popis je důležitý, ale…
Zdroj:
[1] Einsteinův vesmír: Jak vize Alberta Einsteina změnily naše chápání prostoru a času - Kaku, Michio. Nakladatelé: Argo, Dokořán 2005.
Obrázky - všechny vyrobil Bohumír Tichánek, autor tohoto příspěvku na medium seznam cz






